Problem description
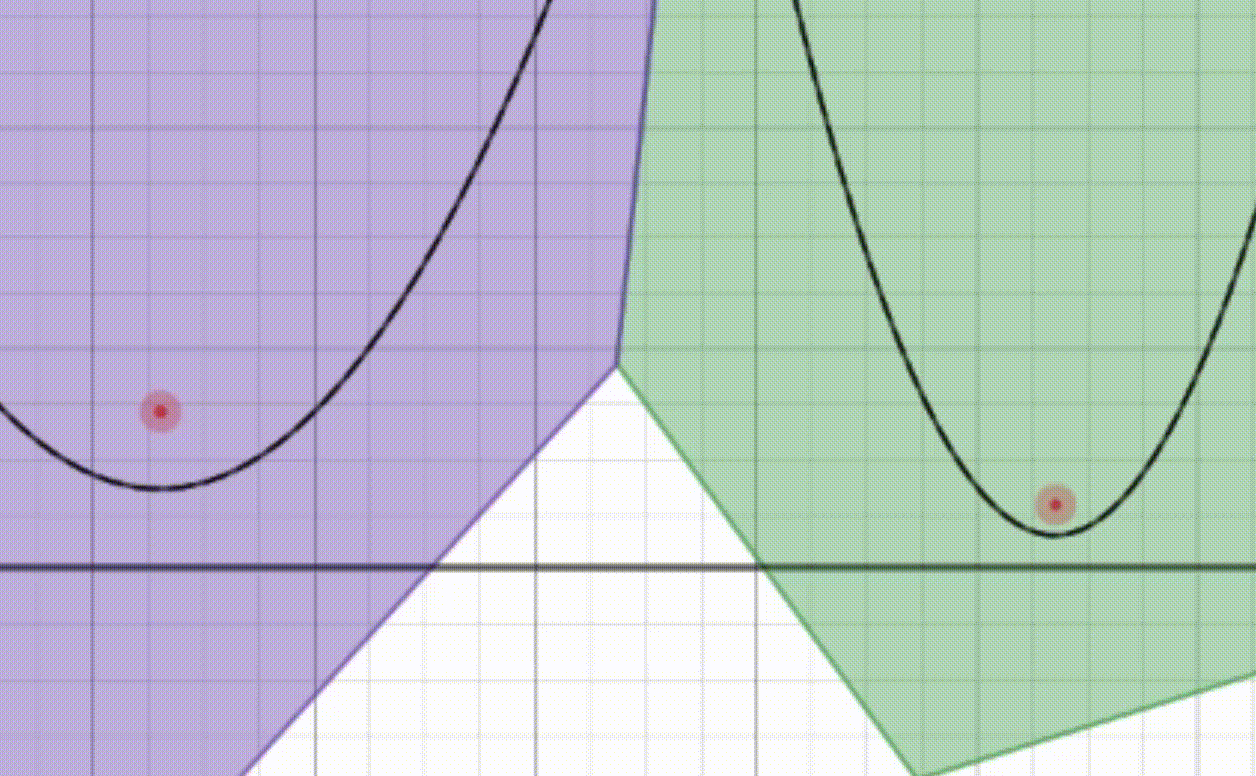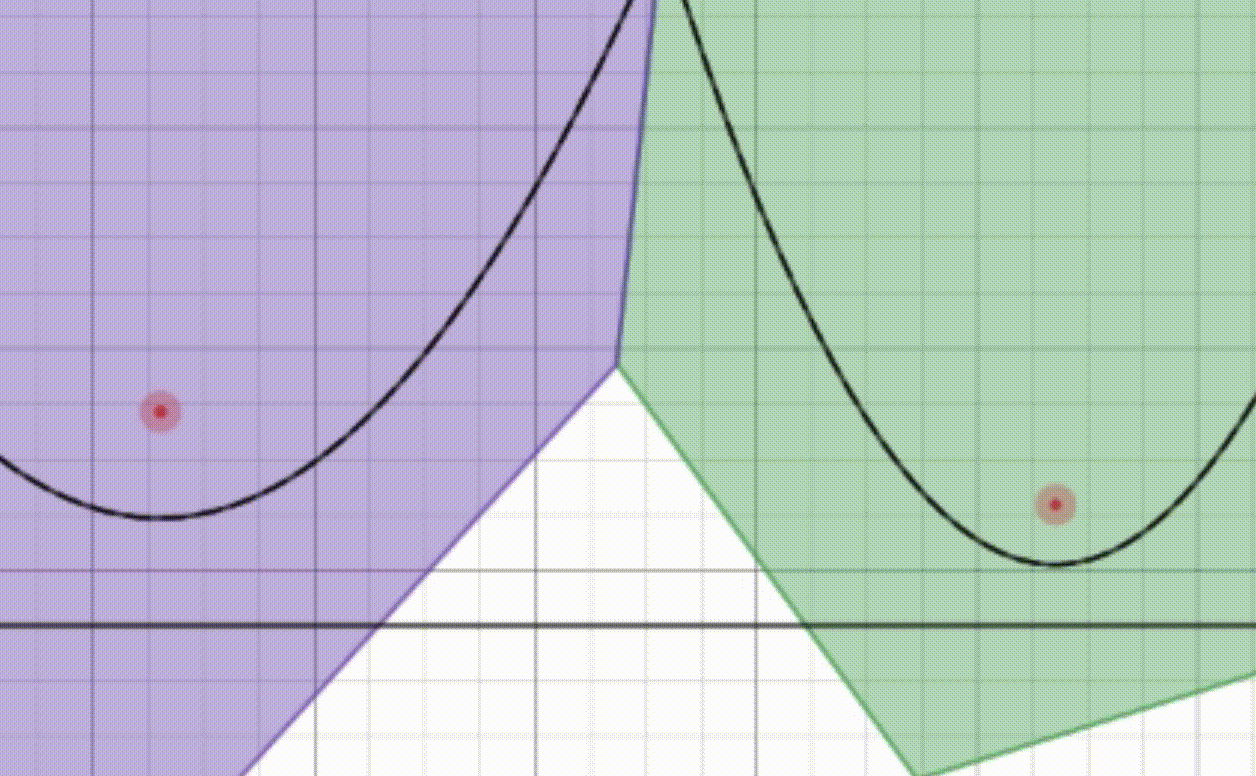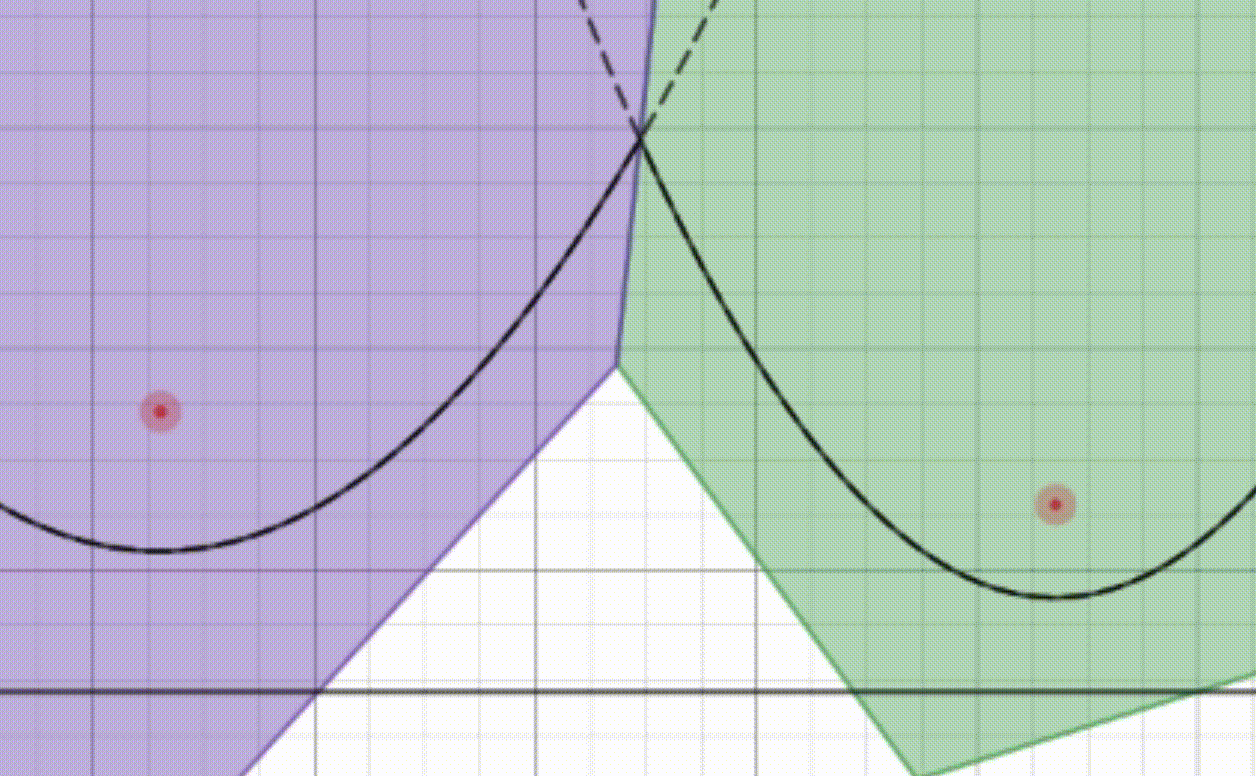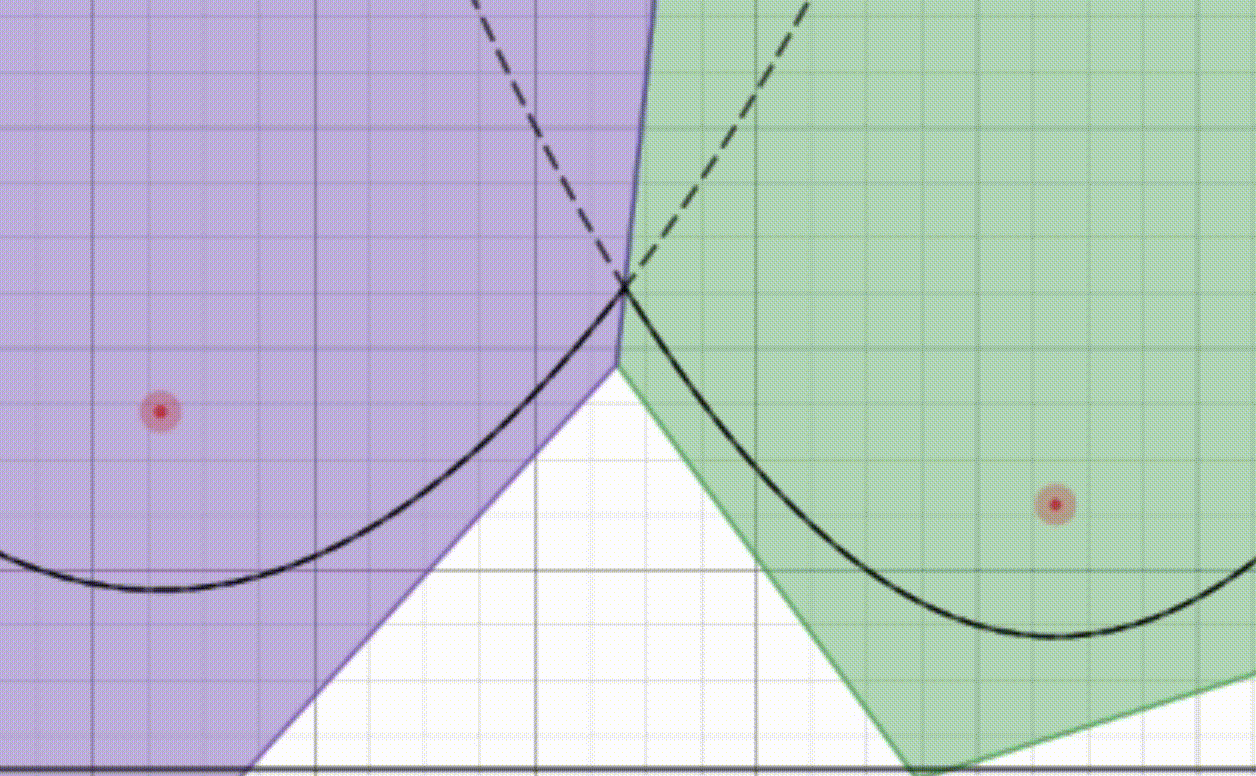
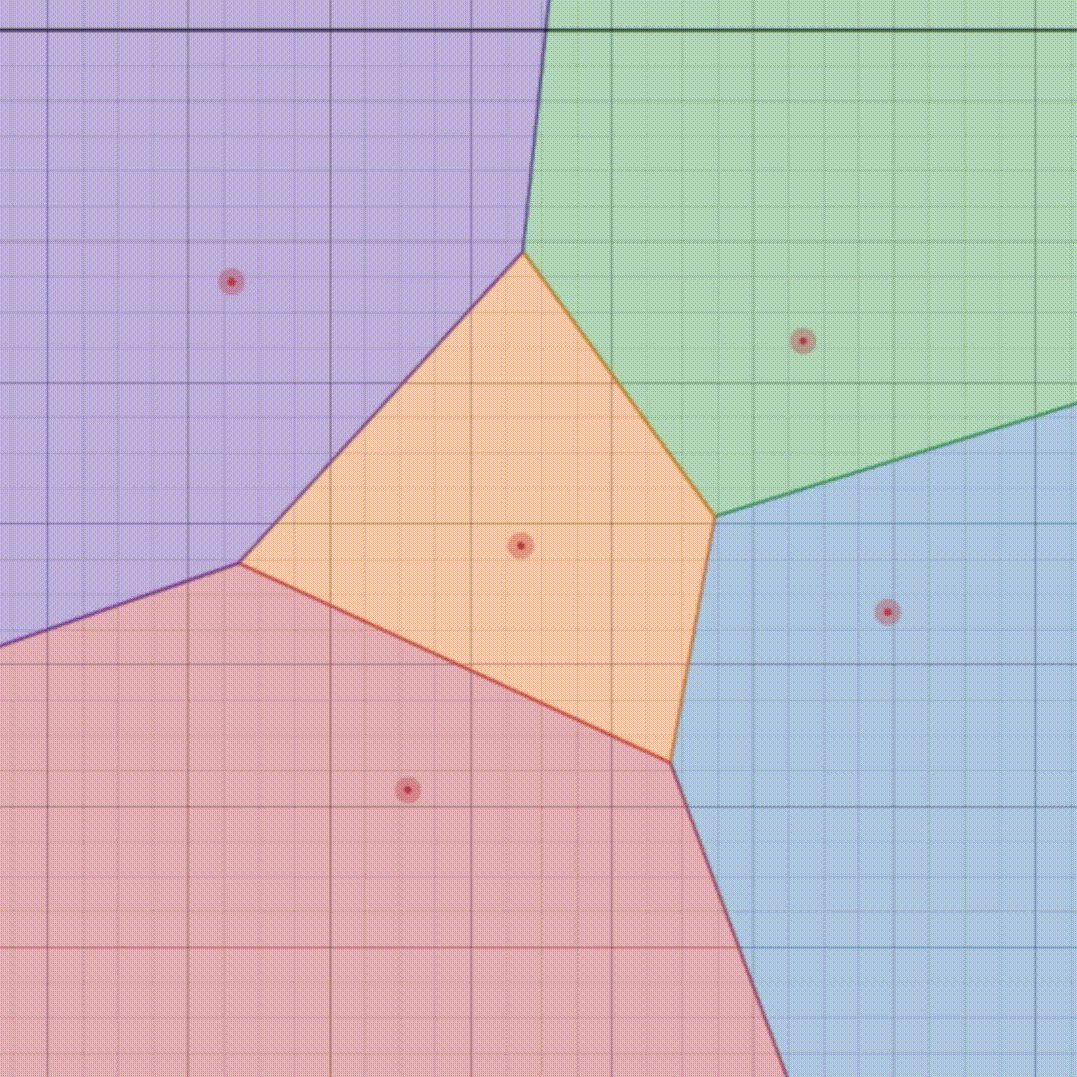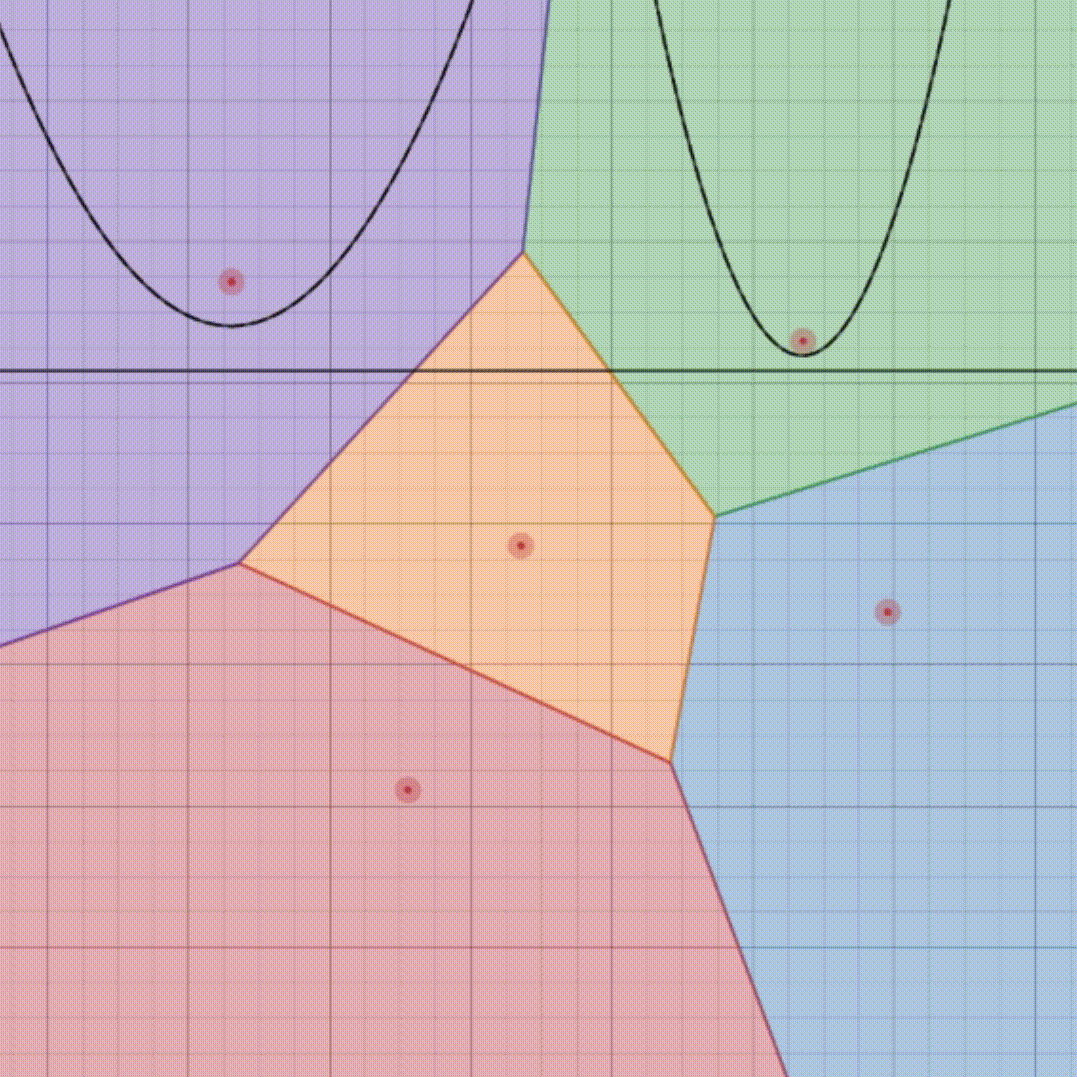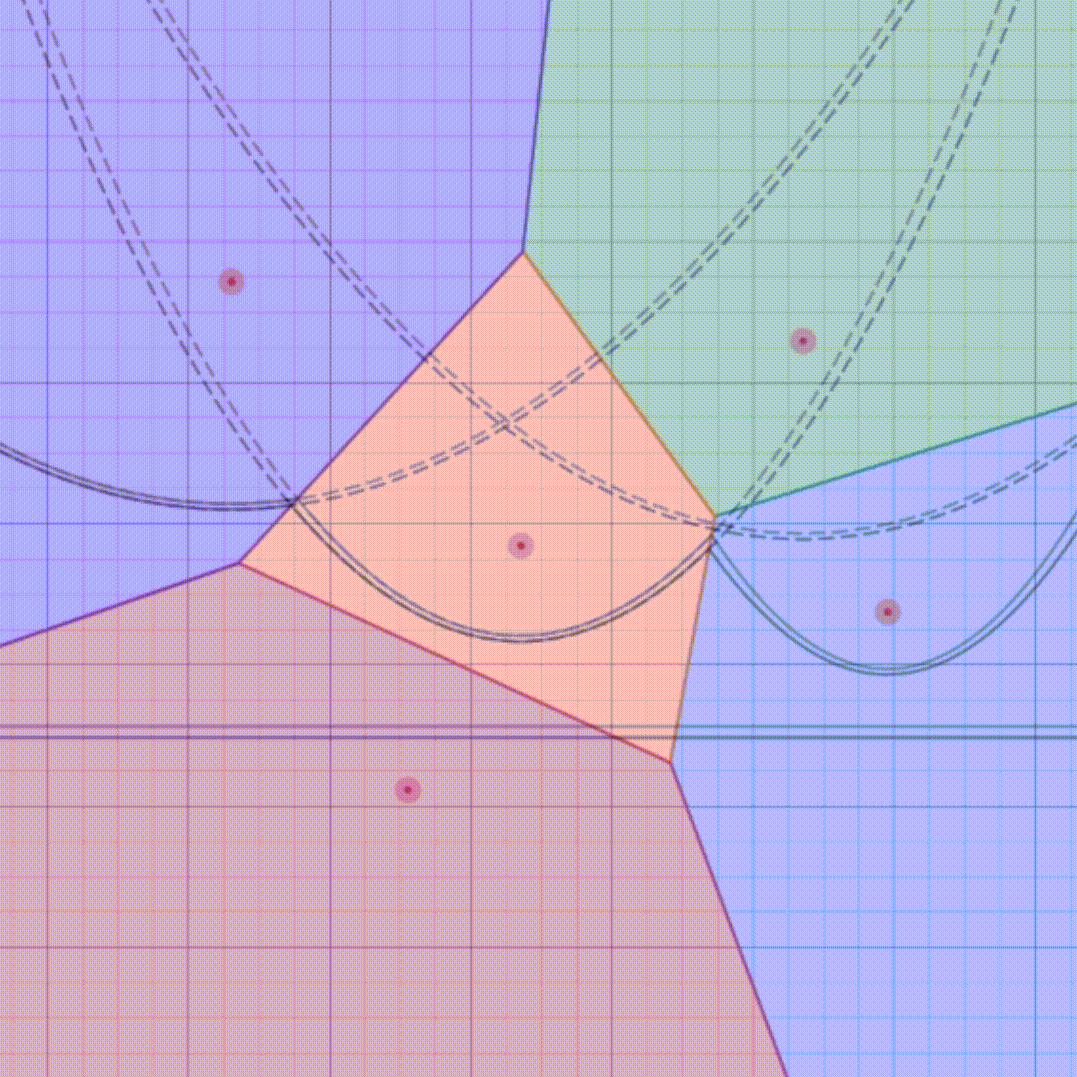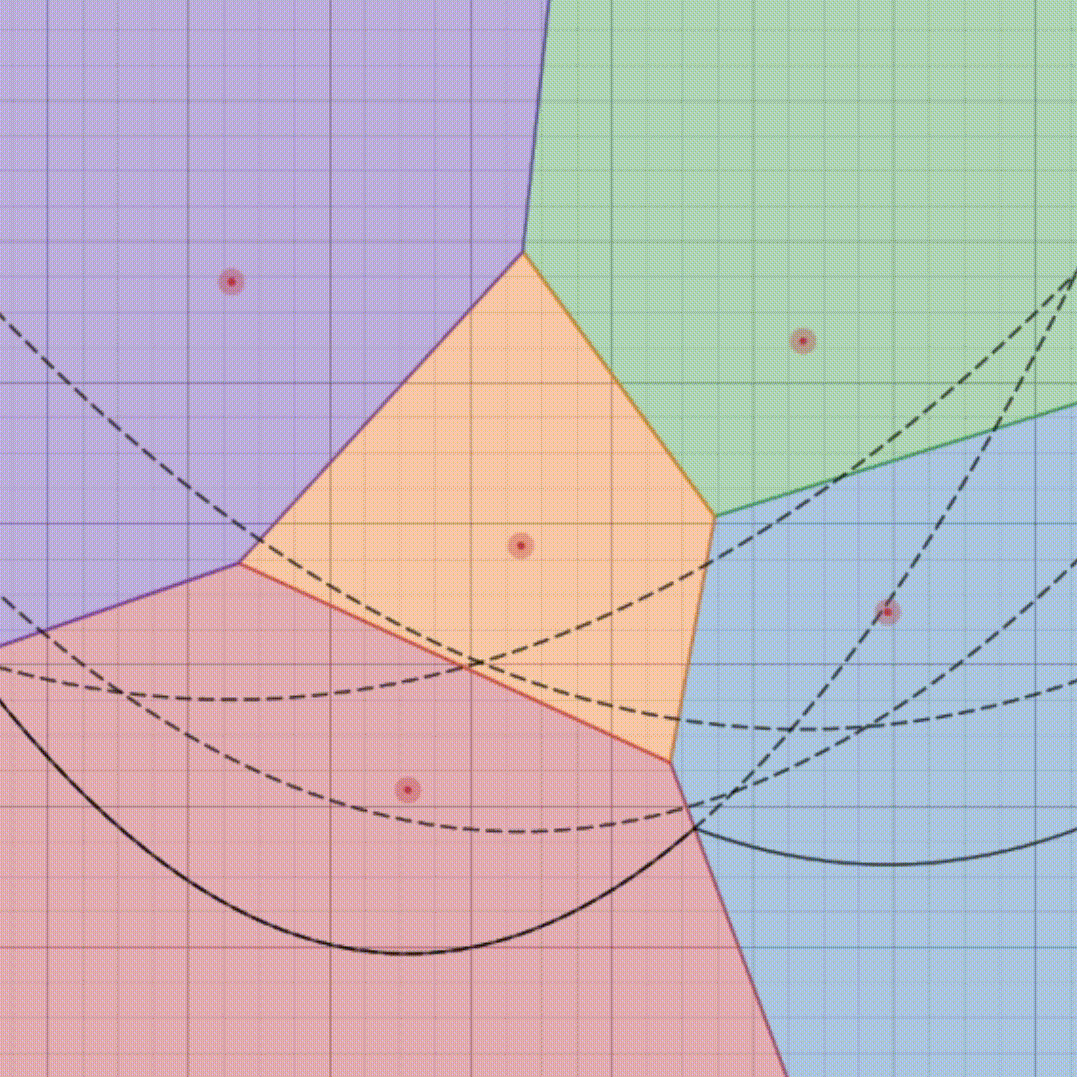
Imagine you have a map of your town with all the ice cream shops marked on it. You and your friends want to find out which ice cream shop is the closest to each of your houses. Instead of checking each shop one by one, you use a special kind of map called a Voronoi diagram.
In this special map, the town is divided into regions, where each region belongs to one ice cream shop. Every point within a region is closer to its corresponding ice cream shop than to any other shop. So, if you’re standing anywhere in a particular region, you know exactly which ice cream shop you should go to because it’s the closest one.
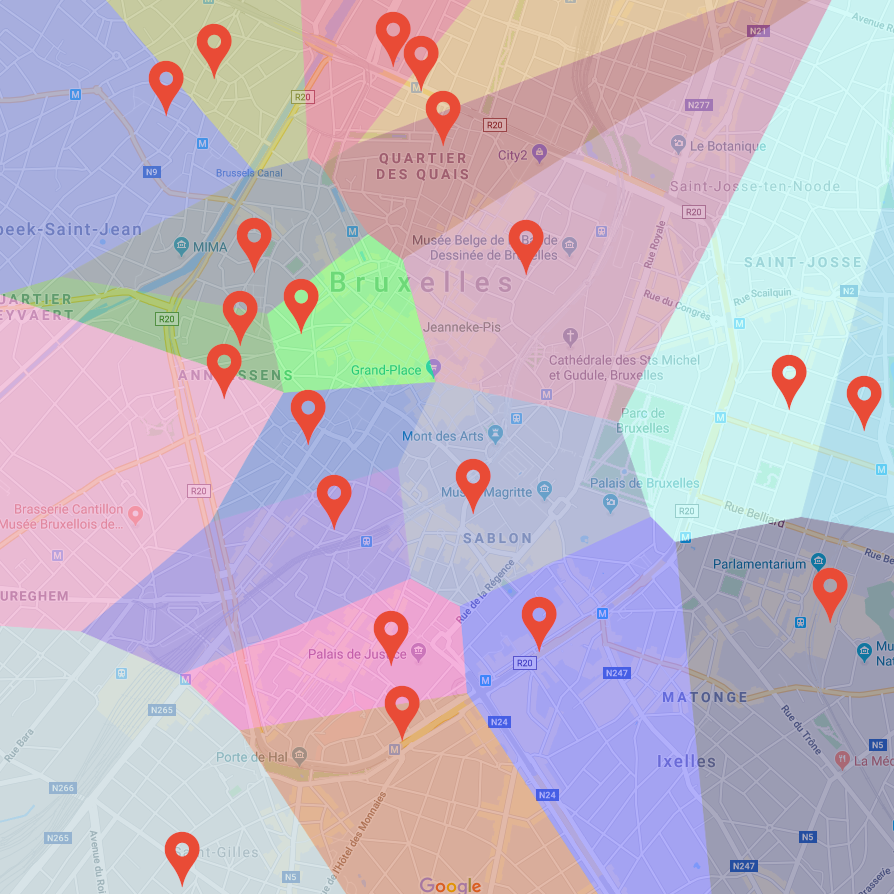
Creating this special map for a large town with many ice cream shops could take a lot of time if done manually. But with the Fortune’s algorithm, we can make this map quickly and efficiently. This algorithm helps us draw the boundaries of each region in such a way that finding the nearest ice cream shop for any location becomes super easy and fast.
So, the Voronoi problem is all about figuring out these regions for a set of points (ice cream shops) on a map, so you can always find out which shop is closest to any given spot in the town.