Network and Cooperation

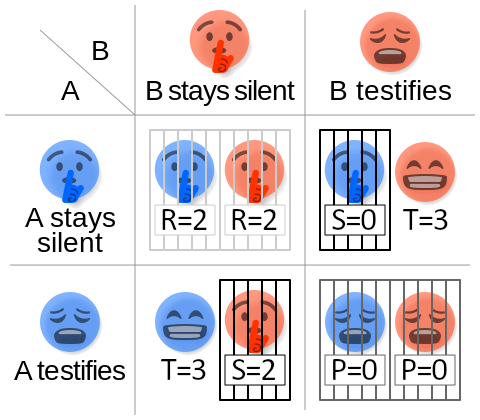
Imagine you and your best friend get caught doing something wrong. You're both taken to separate rooms and can't talk to each other. The police offer you both a deal:

• If you both stay quiet (cooperate with each other), you each get 1 year of punishment.
• If you both tell on each other (betray each other), you each get 2 years of punishment.
• If one of you stays quiet but the other betrays, the one who tells gets no punishment at all, and the one who stayed quiet gets 3 years of punishment.

We say that the Cooperation Reward \(R\) is 2 (since the player get a 2 years discount on the worst penalty, which is 3), the Punishment payoff \(P\) is 1, the Temptation payoff \(T\) is 3, and finally the Sucker's payoff \(S\) is 0.

This situation is tricky because if you stay quiet, you hope your friend does too, so you both get only 1 year. But if you think your friend will tell on you, you might want to tell on him first, so you don't get 5 years while they go free. And you know that your friend is thinking the same way in his room.

We represent this community as a graph, where each node is a player. Each of them is a defector, colored in red, or a collaborator, colored in green.

• At each round, each player is playing a Prisoner's Dilemma game with each of their neighbors, playing the same action (Cooperate or Betray) with each one of them.
• Then, each player will compare his results with one of his neighbors, and mimic is strategy according to this rule: each individual \(i\) chooses randomly one of their direct neighbors \(j\) and with a probability \(P_{ij}\) defined as: $$P_{ij} = \frac{W_j - W_i}{k_{max}D_{max}}$$ where \(W_i\) and \(W_j\) are the payoffs of player \(i\) and \(j\), \(k_{max}\) is the biggest degree between the nodes \(i\) and \(j\), and \(D_{max} = \max(T,R) - \min(S,P)\).